Eigenschaften von Funktionen: Unterschied zwischen den Versionen
| (4 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
| − | Du hast nun Funktionen als Objekte in der Mathematik kennengelernt. | + | Du hast nun Funktionen als Objekte in der Mathematik kennengelernt. Objekte in der Mathematik haben auch Eigenschaften. Du kennst bereits Eigenschaften von Funktionen ohne sie explizit benannt zu haben. Als Nächstes wollen wir die Eigenschaften Monotonie, Symmetrie und Grenzwert von Funktionen betrachten. |
| − | |||
| − | ::[[Funktionen_Einstieg/Monotonie|Monotonie]] | + | :::[[Funktionen_Einstieg/Monotonie|Monotonie]] |
| + | |||
| + | :::::::::[[Funktionen_Einstieg/Symmetrie|Symmetrie]] | ||
| + | |||
| + | :::::::::::::::[[Funktionen_Einstieg/Grenzwert|Grenzwert]] | ||
| − | |||
| − | |||
| Zeile 18: | Zeile 19: | ||
Nun hast du es geschafft, du kennst eine exakte Definition der Funktion und kannst sicher mit Funktionen und ihren Darstellungsformen umgehen. Du hast Eigenschaften von Funktionen kennengelernt und weißt, dass Funktionen mathematische Objekte sind. | Nun hast du es geschafft, du kennst eine exakte Definition der Funktion und kannst sicher mit Funktionen und ihren Darstellungsformen umgehen. Du hast Eigenschaften von Funktionen kennengelernt und weißt, dass Funktionen mathematische Objekte sind. | ||
| − | Eine spezielle Art von Funktionen sind Polynomfunktionen, die einen Ring bilden. | + | Mit Funktionen kann man ähnliche Betrachtungen wie bei Zahlen machen. Eine spezielle Art von Funktionen sind Polynomfunktionen, die einen Ring bilden. Einen algebraischen Ring kennst du mit der Menge der ganzen Zahlen <math> Z </math>. Wie bei den ganzen Zahlen kann man Polynomfunktionen addieren, subtrahieren und multiplizieren. Nur die Division geht wie in der Menge der ganzen Zahlen die Division nicht immer. In diesem Video |
<center>{{#ev:youtube |mPdratwcWMA|350}}</center> | <center>{{#ev:youtube |mPdratwcWMA|350}}</center> | ||
| − | wird diese Problematik angesprochen. Du siehst, dass die Division wie in der Menge der ganzen Zahlen aufgehen oder nicht aufgehen kann. | + | wird diese Problematik angesprochen. Du siehst, dass die Division von Polynomfunktionen ähnlich wie die Division mit ganzen Zahlen funktioniert und - wie die Division in der Menge der ganzen Zahlen - aufgehen oder nicht aufgehen kann. |
| − | <center> Nun weißt du, dass es bei Funktionen noch einiges zum Kennenlernen gibt!</center | + | <center> Nun weißt du, dass es bei Funktionen noch einiges zum Kennenlernen gibt!</center> |
| + | |||
| + | |||
---- | ---- | ||
Zurück zur [[Funktionen_Einstieg|Startseite]] | Zurück zur [[Funktionen_Einstieg|Startseite]] | ||
Aktuelle Version vom 5. Januar 2012, 11:40 Uhr
Zuordnungen - Graph und Wertetabelle - Der Funktionsbegriff - Der Funktionsgraph - Beispiele und Übungen - Eigenschaften von Funktionen
Du hast nun Funktionen als Objekte in der Mathematik kennengelernt. Objekte in der Mathematik haben auch Eigenschaften. Du kennst bereits Eigenschaften von Funktionen ohne sie explizit benannt zu haben. Als Nächstes wollen wir die Eigenschaften Monotonie, Symmetrie und Grenzwert von Funktionen betrachten.
Nun hast du es geschafft, du kennst eine exakte Definition der Funktion und kannst sicher mit Funktionen und ihren Darstellungsformen umgehen. Du hast Eigenschaften von Funktionen kennengelernt und weißt, dass Funktionen mathematische Objekte sind.
Mit Funktionen kann man ähnliche Betrachtungen wie bei Zahlen machen. Eine spezielle Art von Funktionen sind Polynomfunktionen, die einen Ring bilden. Einen algebraischen Ring kennst du mit der Menge der ganzen Zahlen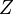 
. Wie bei den ganzen Zahlen kann man Polynomfunktionen addieren, subtrahieren und multiplizieren. Nur die Division geht wie in der Menge der ganzen Zahlen die Division nicht immer. In diesem Video
wird diese Problematik angesprochen. Du siehst, dass die Division von Polynomfunktionen ähnlich wie die Division mit ganzen Zahlen funktioniert und - wie die Division in der Menge der ganzen Zahlen - aufgehen oder nicht aufgehen kann.
Zurück zur Startseite
